图

图片来源于图书馆借的《算法（第 4 版）》一书，为了加深印象，对照书的图用 visio 画了一遍。

图的表示法

邻接矩阵表示法

对于任意图（设其顶点个数为 n），其邻接矩阵是一个 n×n 的二维数组，若 (0, 1) 是 G 的一条边，则其邻接矩阵 a[0][1] =1，若不是，则 a[0][1] = 0 。而且无向图的邻接矩阵一定是对称的。无向图的邻接矩阵只需存储其上三角或者其上三角部分。

对于一个有向图，顶点 i 所对应的 行中的数字之和等于顶点 i 的出度 ，对应的 列中的数字之和等于顶点 i 的入度 。

邻接表表示法

对于有 n 个结点，e 条边的无向图，采用邻接表存储表示需要存储 n 个头结点和 2e 个表结点 ，每个结点有两个域。同时，对于有 n 个结点，e 条边的无向图，可以在 \(O(n+e)\) 时间内确定无向图中边的总数。而对于有向图，通过对某个顶点的链表中的结点计数，可以得到该顶点的出度，但是对于该顶点的入度很难确定

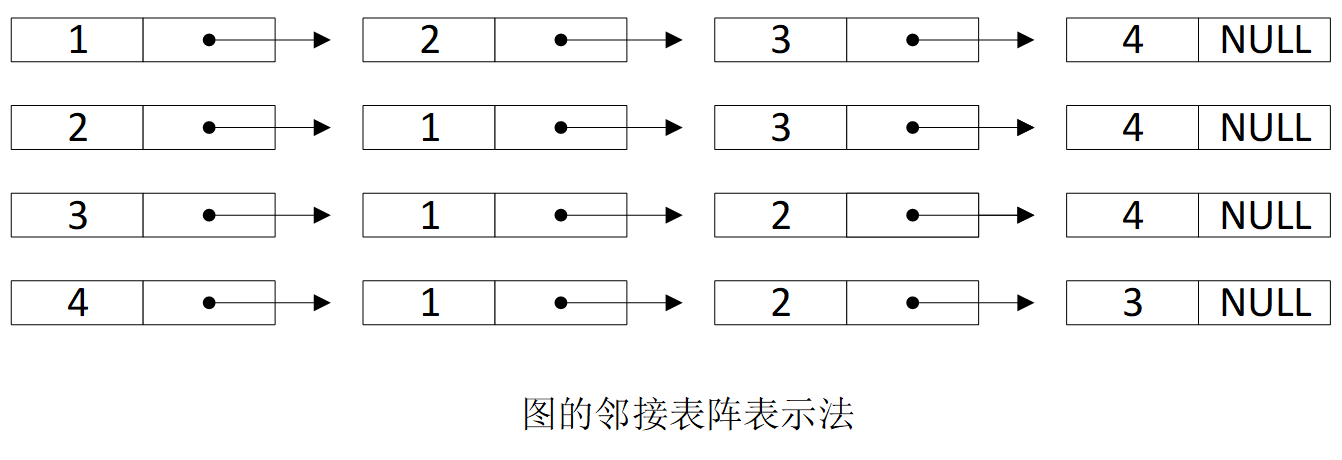
data_structure_graph_adjoin_table_1.png

邻接矩阵与邻接表相互转换

void Trans_MtoL(Mgraph G, Lgraph Gl) {
    Vnode *p, *q;
    int e, i, j;
    for (i = 1; i <= n; i++) {
        Gl[i].data = i;
        Gl[i].next = NULL;
    }
    for (i = 1; i <= n; i++) {
        for (j = i+1;j <= n && G[i][j] == 1; j++) {
            p = (Vnode *)malloc(sizeof(Vnode));
            p->data = i;
            p->next = Gl[j].next;
            Gl[j].next = p;
            q = (Vnode *)malloc(sizeof(Vnode));
            q->data = j;
            q->next = Gl[i].next;
            Gl[i].next = q;
        }
    }
    printf("邻接矩阵表示如下：\n");
    Output_mg(G);
    printf("\n 邻接表表示如下 ：");
    Output_L(Gl);
}

void Trans_LtoM(Lgraph Gl, Mgraph G) {
    Vnode *p;
    int i, j;
    for (i = 1; i <= n; i++)
            for (j = 1; j <= n; j++)
                G[i][j] = 0;
    for (i = 2;i <= n; i++) {
        p = Gl[i].next;
        while (p != NULL) {
            j = p->data;
            G[i][j] = 1;
            G[j][i] = 1;
            p = p->next;
        }
    }
    printf(" 邻接表表示如下 ：\n");
    Output_L(Gl);
    printf("\n邻接矩阵表示如下：");
    Output_mg(G);
}

其他表示法

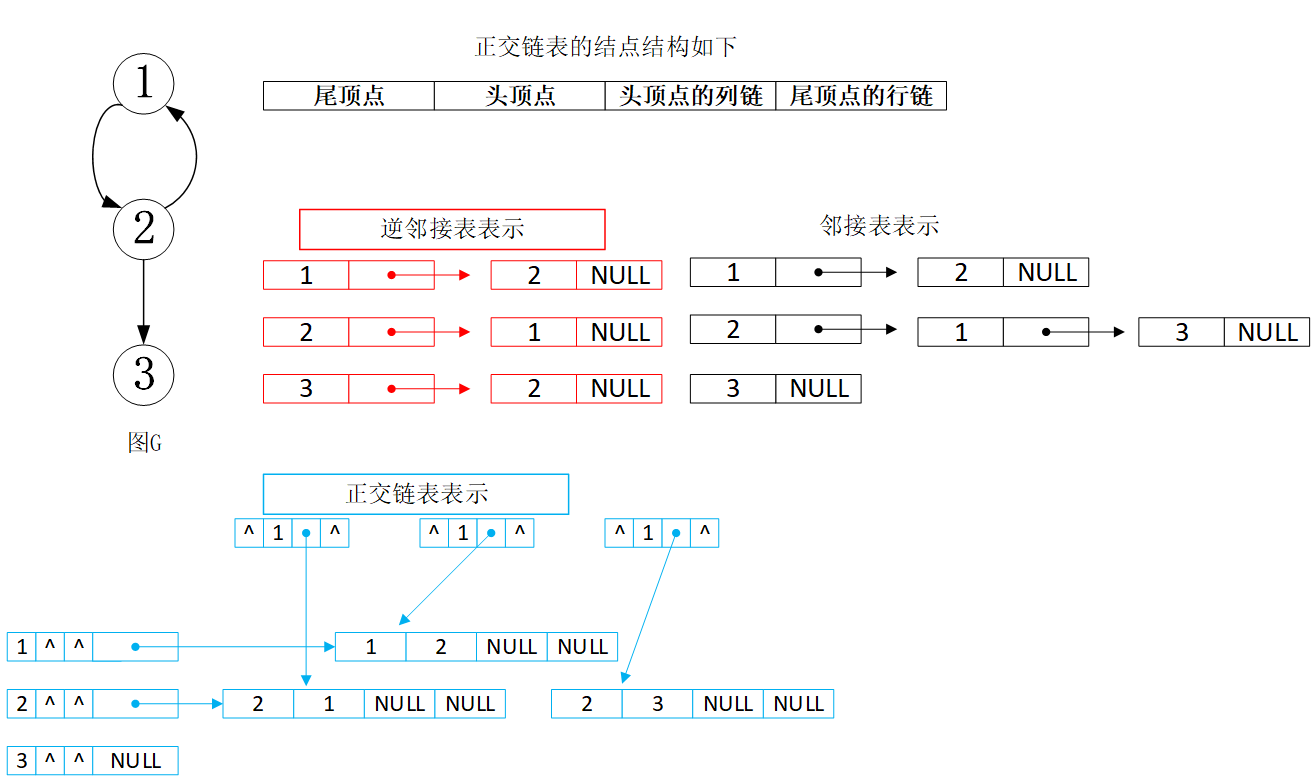
data_structure_graph_mixed_expression_1.png

图的遍历方法

深度优先遍历

  1. 在访问一个顶点时，将它标记为已访问
  2. 递归地访问它的所有没有标记的邻居顶点

优先搜索访问起始顶点 a，然后从顶点 a 的邻接表中选取一个未访问过的结点 b 进行访问，并从 b 开始继续进行深度优先搜索。这个过程会将 a 的邻接表中的当前位置保存在一个栈中，当最终搜索到一个顶点 z，且 z 的邻接表中的结点全部被访问过时，就从这个栈中取出一个顶点，并按照上述方法处理该顶点的邻接表。在此搜索过程中，已经访问过的顶点不再被访问，而未被访问的顶点被访问且存入栈。当栈为空时，搜索就结束了。这些过程可以很容易使用递归来实现。最坏时间复杂度为 \(O(n+2e)\)

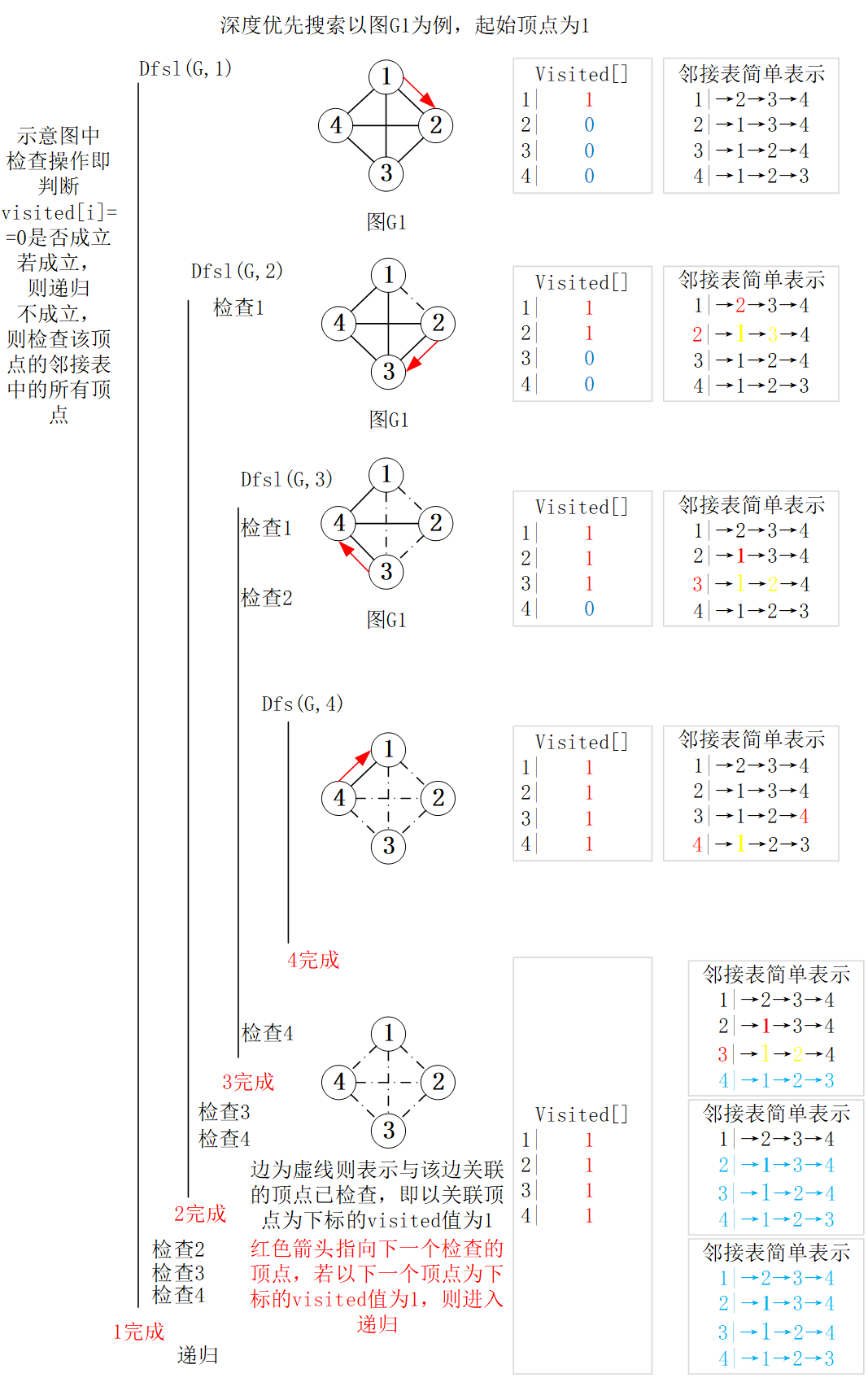
data_structure_graph_depth_first_traversal_1.png
  • 参考代码
void Dfs(Mgraph G ,int v) {
    int i;
    printf("%d -> " ,v);
    visited[v] = 1;
    for (i = 1 ;i <= n && G[v][i] == 0;i++)
        ;
    for (; i <= n; i++)
        if(visited[i] == 0)
            Dfs(G, i);
}

广度优先遍历

  1. 取队列中的下一个顶点 a 并标记它
  2. 将和 a 相邻的所有为被标记过的顶点加入队列

从访问起始顶点 a 开始，并把 a 标记为已访问，然后，访问 a 的邻接表中的每一个顶点。在访问过 a 的邻接表中所有顶点后，访问与 a 的邻接表中的第一个顶点相邻，且未被访问过的所有顶点。这样就需要一个队列，把当前访问的顶点保存在这个队列中，在当前顶点的邻接表中的有顶点被访问过时，从队列中取出一个顶点，然后访问该顶点的邻接表中的所有顶点。在此搜索过程中，未被访问的顶点被访问，且存入队列，已经访问过的顶点不再被访问。当队列为空时，搜索就结束了。时间复杂度量级为 \(O(n^2)\)

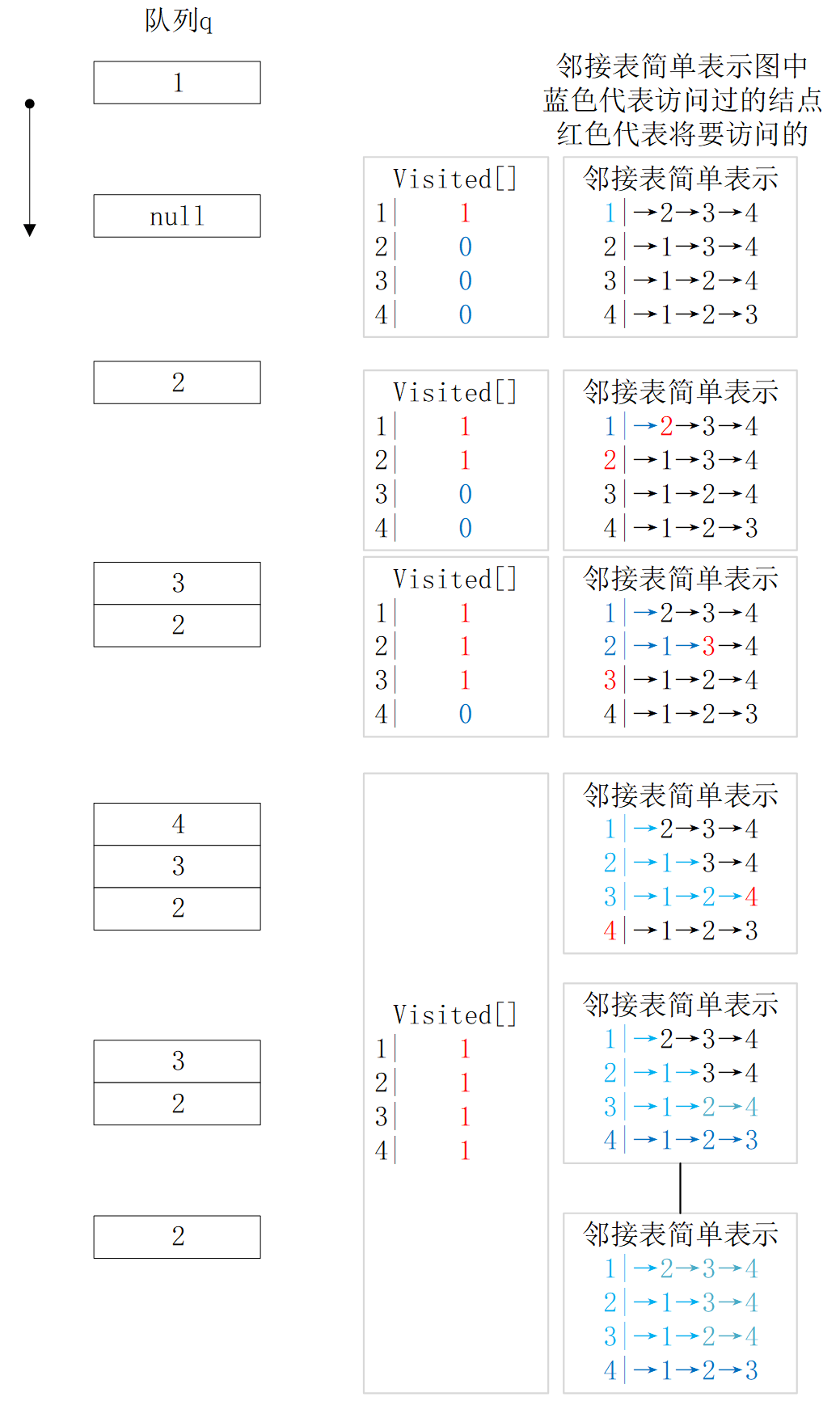
data_structure_graph_breadth_first_traversal_1.png
  • 参考代码
void Bfs(Mgraph G, int v) {
    int i;
    Queue *Q = (Queue *)malloc(sizeof(Queue));
    Initqueue(Q);
    printf("%d ->" ,v);
    visited[v] = 1;
    enqueue(Q, v);
    for (; !quempty(Q); ) {
        v = dequeue(Q);
        for (i = 1;i <= n; i++) {
            if (visited[i] == 0 && G[v][i] == 1) {
                printf("%d ->", i);
                visited[i] = 1;
                enqueue(Q, i);
            }
        }
    }
}

拓扑排序

typedef struct GNode {
    int Cnt; // 计数
    int Tag; // 标签
    int Vertex;
    struct GNode *Link;
} GNode;

typedef GNode Graph[MAX];

void Topsort(Graph G ,int n) {
    GNode *p;
    int i, j, k, top =- 1;
    for (i = 1 ;i <= n; i++) {
        if(G[i].Cnt == 0) {
            G[i].Cnt == top;
            top = i;
        }
    }
    for (i = 1 ;i <= n; i++) {
        if (top == -1) ;
        else {
            j = top;
            top = G[top].Cnt;
            printf("%d ->",j);
            for (p = G[j].Link; p; p = p->Link) {
                k = p->Vertex;
                G[k].Cnt--;
                if (G[k].Cnt == 0) {
                    G[k].Cnt = top;
                    top = k;
                }
            }
        }
    }
}
湘ICP备19014083号-1